114/10/29
一滴血能看見未來嗎?液態切片把血液變成你的「健康雷達」
李依庭|
科技大觀園特約編輯
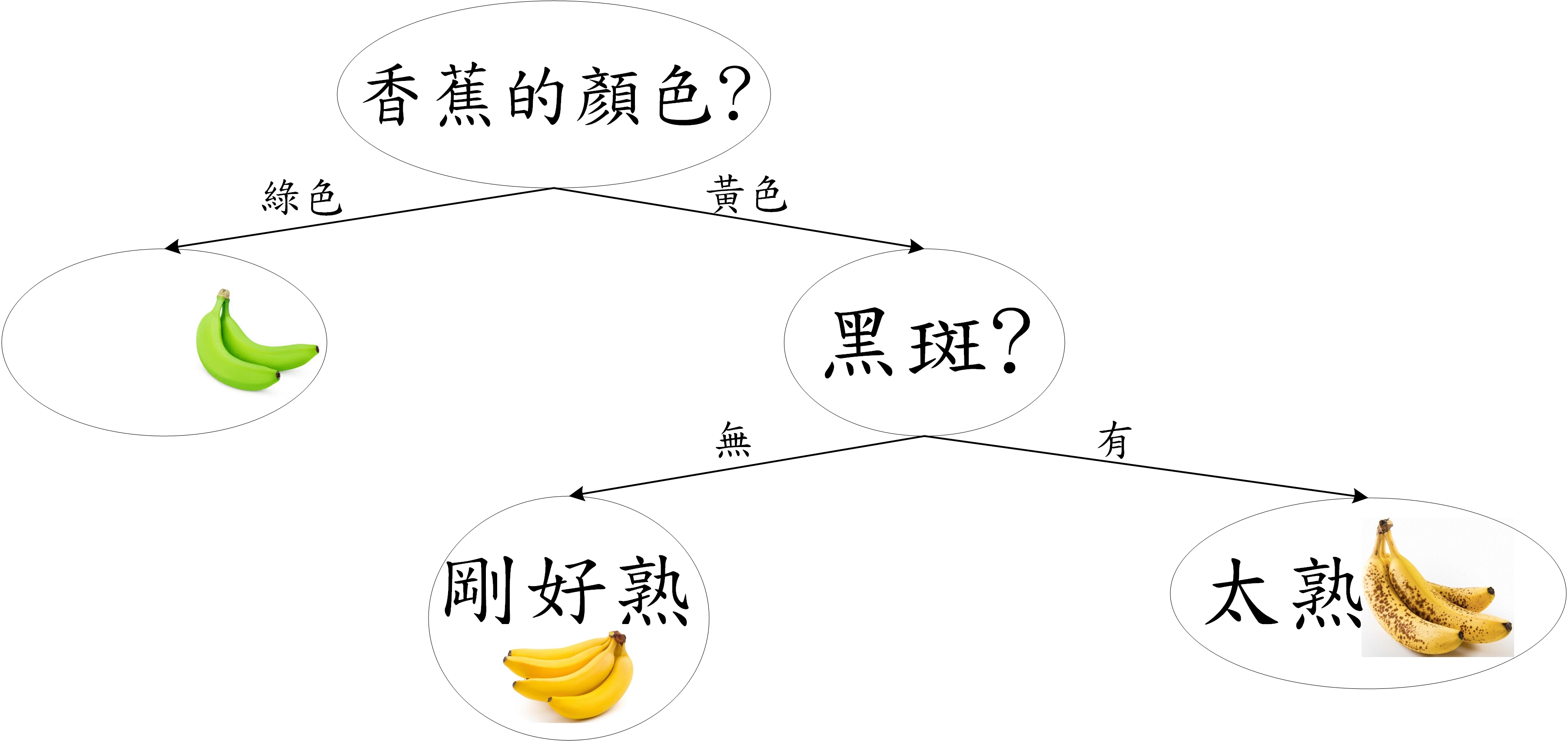
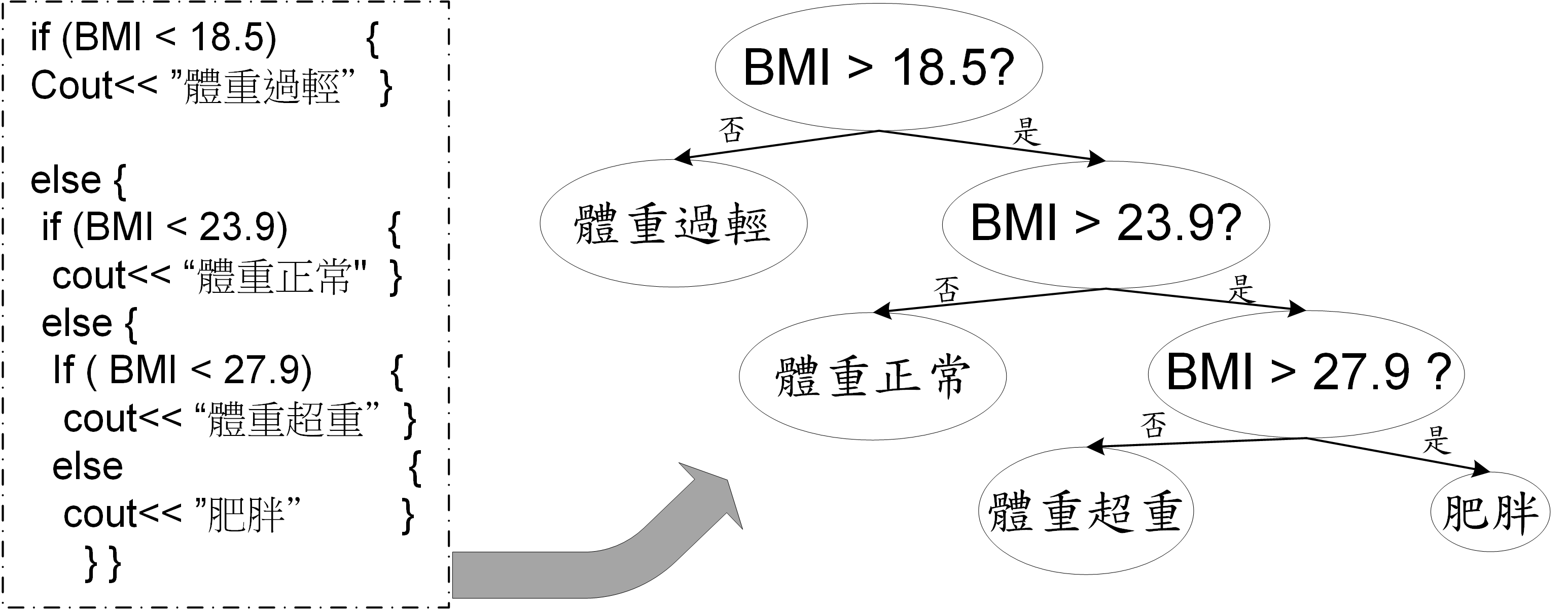 透過決策樹,可以把左側巢狀的程式語言製作成右側淺顯易懂的樹狀圖(圖片來源:簡伯丞)
透過決策樹,可以把左側巢狀的程式語言製作成右側淺顯易懂的樹狀圖(圖片來源:簡伯丞)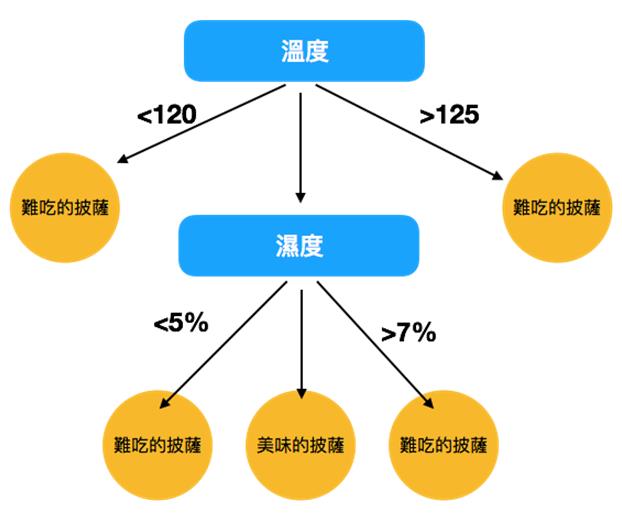 從該圖的決策樹中,我們可以判斷出溫度在120~125°C及濕度在5~7%時可以做出美味的披薩。(圖片來源:Medium/網址:https://medium.com/@yehjames)
從該圖的決策樹中,我們可以判斷出溫度在120~125°C及濕度在5~7%時可以做出美味的披薩。(圖片來源:Medium/網址:https://medium.com/@yehjames)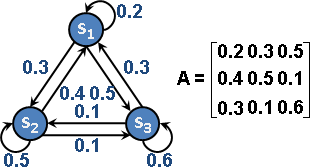 一個簡單的馬可夫鏈,由S1, S2, S3三個狀態組成;右邊的矩陣則是將這些狀態之間的每一個機率做成一個馬可夫鏈的「轉移矩陣」。(圖片來源:演算法筆記/網址:http://www.csie.ntnu.edu.tw/~u91029/State2.html)
一個簡單的馬可夫鏈,由S1, S2, S3三個狀態組成;右邊的矩陣則是將這些狀態之間的每一個機率做成一個馬可夫鏈的「轉移矩陣」。(圖片來源:演算法筆記/網址:http://www.csie.ntnu.edu.tw/~u91029/State2.html)決策樹概念簡單,並且具有強大的實用性。實務上在使用決策樹時,可依需求搭配適合的演算法進而增進效率。當然,決策樹的建立方法百百種,如何找到適合自己研究的建立方法才是最重要的。
副總編輯:國立中山大學資訊工程學系 陳坤志教授
總編輯:國立中山大學資訊工程學系 黃英哲教授
(本文由科技部補助「新媒體科普傳播實作計畫」執行團隊撰稿)