桌上有一顆夜明珠。關掉電燈夜明珠在黑暗中可以發出光芒 (圖一)。這是一種磷光現象。在討論磷光現象之前,老師要先介紹一些量子物理的基礎知識。
 圖一。
圖一。1924 年 Louis de Broglie 提出了物質波假設。他認為物質也會表現出波動的行為。Erwin Schrodinger 第一次聽到 Louis de Broglie 的假設時認為是荒誕無稽之說。但是當他知道 Einstein 很認真地看待Louis de Broglie 的假設時,他決定尋找描述物質波的方程式。1925年Erwin Schrodinger發表了物質波方程式,奠定了量子物理的基礎。
依據 Schrodinger 方程式,原子中電子的狀態可用 3 個量子數確定:主量子數、軌域角動量量子數、及軌域磁量子數。原子物理學家利用高解析度光譜儀研究鈉原子光譜,發現 589.3nm 的譜線包含589.0nm 及 589.6nm 兩條譜線。許多原子的譜線都存在此種精細結構。Schrodinger 方程式可解釋許多原子光譜的性質,但無法解釋精細結構。
1925 年 Wolfgang Pauli 提出了解釋原子光譜精細結構的構想。如果電子存在第 4 個量子數,而且此量子數只有 2 個可能的數值,原子光譜的精細結構便可得到合理的解釋。受到 Wolfgang Pauli 的啟發,S. A. Goudsmit 與 E. Uhlenbeck 在 1925 年提出了電子自旋的概念。電子除了繞原子核運動的軌域角動量外,還有自旋角動量。自旋角動量只有 2 個可能的數值1/2?或-1/2?,其中? =h/2π。 h為 Planck 常數,其數值為
h = 6. 626 × 10-34J ? s
S. A. Goudsmit 與 E. Uhlenbeck 將電子想像為繞著直徑旋轉的帶電球(圖二)。電子自旋角動量的方向只能向上或向下。自旋向上及自旋向下的角動量分別為1/2?及 ?1/2?。這種描述雖然方便,但並不正確。電子是質點,無法自旋。1929 年 Paul Dirac 結合特殊相對論與量子力學提出了相對論性物質波方程式。電子自旋的概念在 Dirac 方程式中很自然地出現。因此電子自旋是在相對論時空結構中的性質,無古典對應。依據 Dirac 方程式,電子自旋量子數為1/2,自旋磁量子數為±1/2。正號及負號分別代表自旋向上和自旋向下。
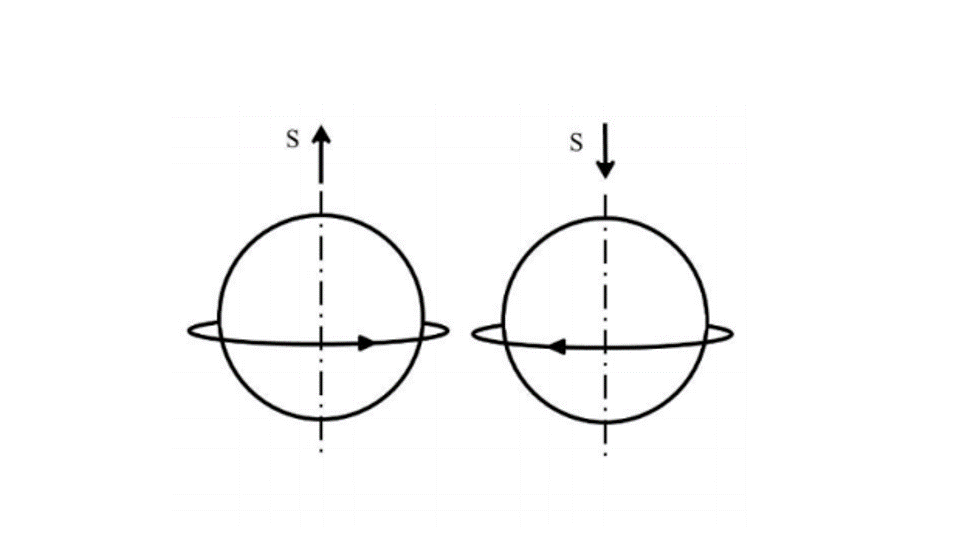 圖二。
圖二。原子光譜的精細結構是自旋軌道耦合造成的。電子自旋產生自旋磁矩。從原子核的座標系來看,電子繞著原子核運動(圖三)。從電子的座標系來看,帶正電的原子核繞電子運動產生磁場(圖四)。電子的自旋磁矩與磁場作用產生位能。自旋向上和自旋向下產生不同的位能,因而使原子譜線分裂。
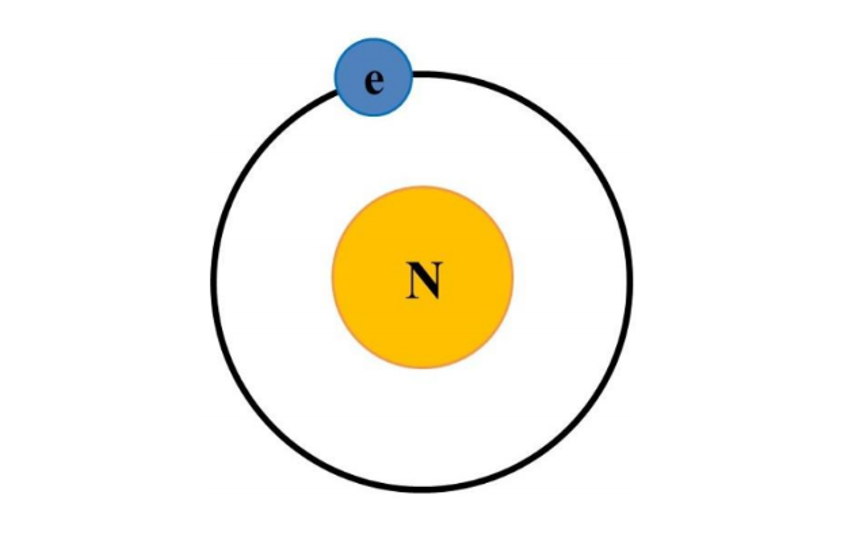 圖三。
圖三。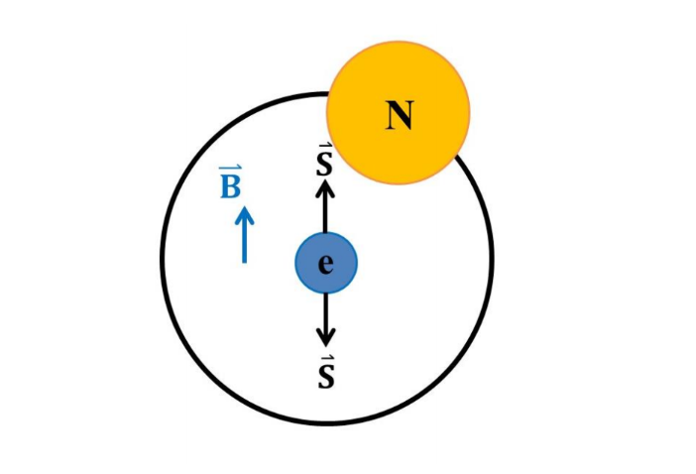 圖四。
圖四。從以上的討論可知原子中電子的狀態可用 4 個量子數確定:主量子數、軌域角動量量子數、軌域磁量子數、及自旋磁量子數。電子的軌域角動量相加得到原子的軌域角動量。電子的自旋角動量相加得到原子的自旋角動量。我們可用原子的軌域角動量量子數、軌域磁量子數、自旋量子數、及自旋磁量子數描述原子的狀態。不同的原子狀態通常具有不同的能量。因此我們將原子狀態稱為能階。原子能階是不連續的。
接下來我們介紹原子能階間的躍遷。原子躍遷可分為二種:輻射躍遷及非輻射躍遷。在輻射躍遷過程中,原子吸光從低能階升至高能階,或者放光從高能階降至低能階。輻射躍遷必須符合選擇定則。如果不考慮自旋軌道藕合,只有具相同自旋量子數的能階間才可產生躍遷。非輻射躍遷最主要的機制是原子碰撞。原子可經由碰撞獲得或損失能量。
在圖五中,我們分別用 S 及 T 表示自旋量子數為 0 及 1 的能階。原子的基態 S0及激發態 S1自旋量子數相同,符合選擇定則,可產生輻射躍遷。處於基態S0的原子吸光升至激發態S1。處於激發態 S1的原子可放光回到基態S0,放出的光稱為螢光。螢光過程發生極快,在10-8秒內即可發生。因此入射光停止後螢光過程也立即停止。我們在電子荷質比(二)單元中看到的綠色光圈就是螢光。處於激發態S1的原子也可經由非輻射躍遷降至激發態 T1。激發態T1與基態 S0的自旋量子數不同,不符合輻射躍遷的選擇定則。如果沒有自旋軌道藕合效應,T1 與 S0 間不會產生輻射躍遷。自旋軌道藕合效應使處於 T1的原子可放光回到S0,放出的光稱為磷光。自旋軌道藕合效應很微弱,因此磷光過程的發生機率很小。處於T1的原子生命期很長,因此T1稱為暫穩態。入射光停止後仍然有許多原子處於暫穩態,因此磷光過程持續存在。這就是夜明珠在黑暗中仍可發光的原因。同學如果想進一步了解磷光現象,可參考 Mitchel Weissbluth 所著 Atoms and Molecules。
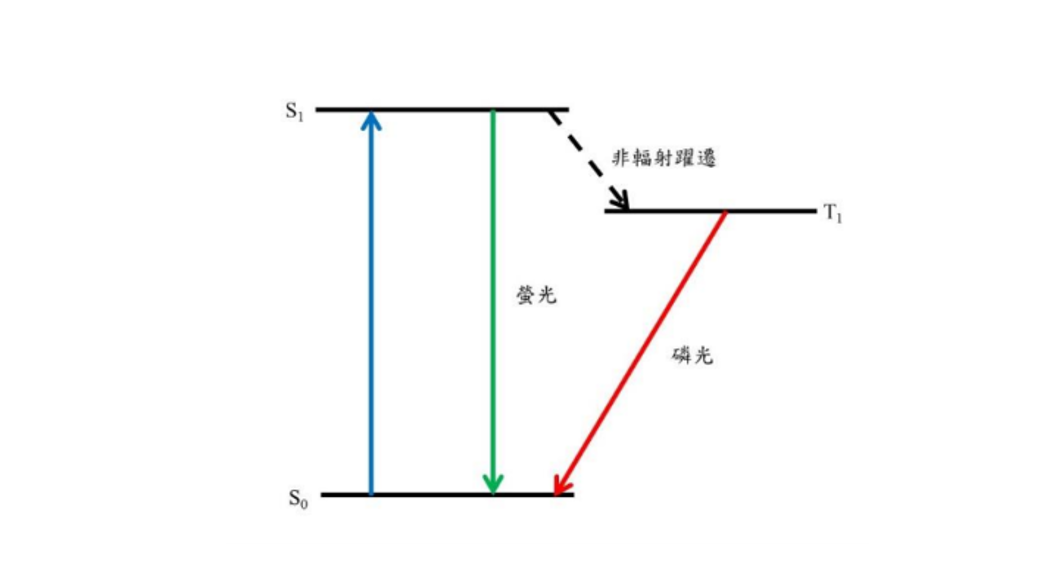 圖五。
圖五。



