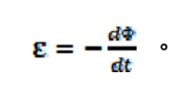桌上有一台具海洋特色的物理教具(圖一)。教具上有一艘小船,船身下方有螺線管。磁鐵固定在教具上。船順流而下。當船身下方的螺線管通過磁鐵時船身上的燈泡會發光,船會減速停止。對船施力船才會繼續運動。這是一種電磁感應現象。
 圖一。
圖一。我們用一個簡單的例子說明電磁感應。在圖二中,長度為L的金屬棒以等速度

在 U 字型金屬軌道上向右滑動。軌道上有電阻 R。均勻磁場B垂直軌道面向內。在「電荷在磁場中的運動」及「電子荷質比(一)(二)」單元中,我們說過電量q速度

的粒子在磁場中所受磁力為:
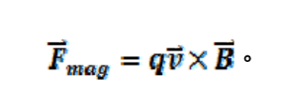 式(1)。
式(1)。因此金屬棒上電子受磁力作用。磁力在垂直方向的分量使金屬棒上的電子向下運動。金屬棒產生向上電流。
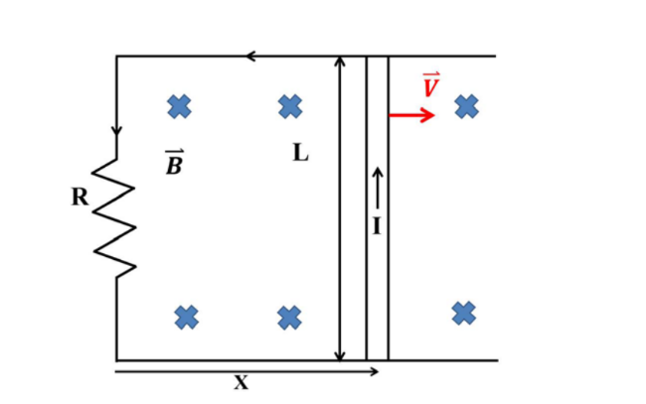 圖二。
圖二。在圖三中,我們繪出金屬棒上電子的速度及受力。當金屬棒上的電子沿金屬棒向下運動時,電子除了水平速度

以外,還有垂直向下的速度

。因此電子相對於地面的速度為
。w與金屬棒夾角為θ,因此:
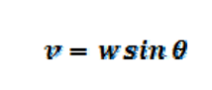 式(2)。
式(2)。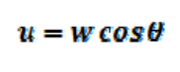
電子所受磁力為
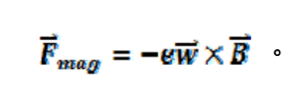
磁力在垂直方向的分量為
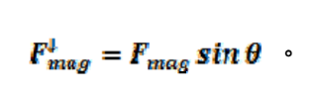 式(5)。
式(5)。將(4)式代入 (5)式得
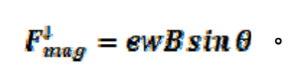 式(6)。
式(6)。再將(2)式代入 (6)式得
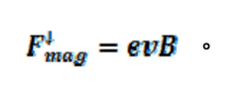 式(7)。
式(7)。我們在前面說過磁力在垂直方向的分量使金屬棒產生電流。磁力在水平方向的分量為
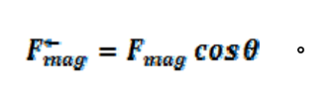 式(8)。
式(8)。將(4)式代入 (8)式得
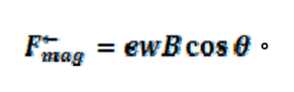
再將(3)式代入(9)式得
式(9)。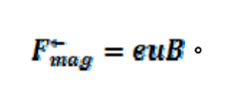 式(10)。
式(10)。磁力水平分量向左,使金屬棒減速。若要使金屬棒等速運動,必須對電子施向右拉力
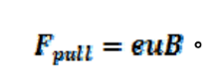 式(11)。
式(11)。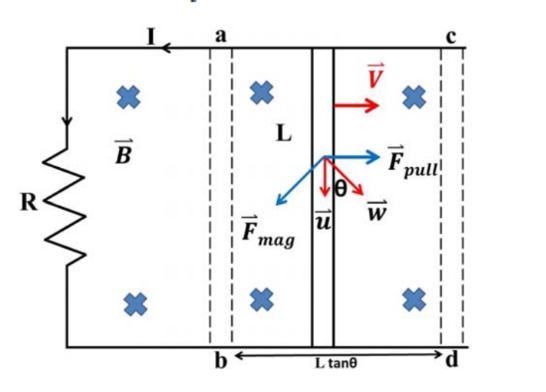 圖三。
圖三。金屬棒上電子受磁力作用向下運動。U 字型金屬軌道有電阻,此電荷集中在金屬棒上下兩端。金屬棒上端帶正電下端帶負(圖四)。正負電荷分開使金屬棒產生向下電場E 。電子受到向上靜電力F = -eE。當向上靜電力等於向下磁力時,金屬棒上電子受力為零,達到平衡態。此時 E+v×B = 0。因此平衡態時靜電場大小為E = vB。金屬棒上下兩端電位差為
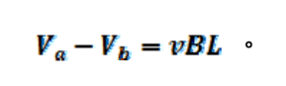
運動金屬棒在金屬軌道上產生逆時鐘方向電流
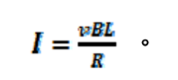 式(13)。
式(13)。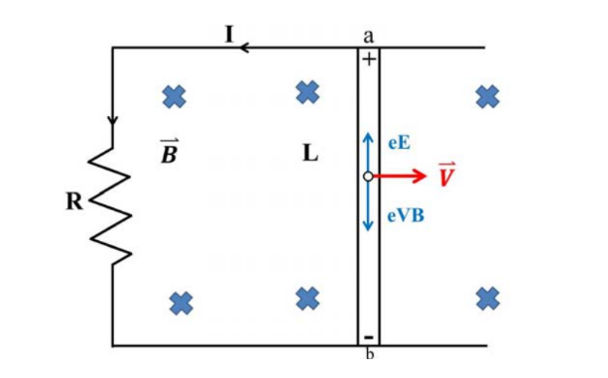
在金屬棒外,電子從 b 點運動至a點,電子電位能減少,外界不須做功。在金屬棒內,電子從a點運動至 b 點,電子電位能增加。要使電子電位能增加,外界必須對電子做功。是什麼力對電子做功呢?由(4) 式可知磁力與電子速度垂直,因此磁力不會對電子做功。由圖三知拉力與電子速度w的夾角為π/2 - θ。因此拉力可對電子做功。假設
金屬棒在ab位置時電子在a點。金屬棒運動至cd位置時電子運動至d點。電子水平位移為L tan θ。拉力對電子做功為
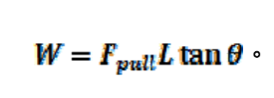
將(2)、(3)、(11)式代入(14)式得
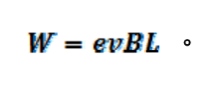 式(15)。
式(15)。
外力使單位電荷沿封閉路徑運動一圈所做的功稱為電動勢。由(15)式知拉力在金屬棒及金屬軌道建立的電動勢大小為
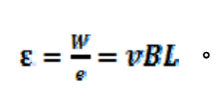 式(16)。
式(16)。
此電動勢為金屬棒在磁場中運動所造成,因此稱為動生電動勢。比較(12)式與(15)式可知
式(12)。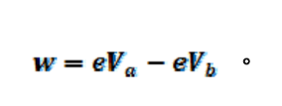 式(17)。
式(17)。
等號右邊是電子電位能改變。在「達文西攻城加農砲」及「雲霄飛車(二)」單元中,我們介紹過功能定理。依據功能定理,拉力對電子做功等於電子動能改變加位能改變。在平衡態,金屬棒上電子受力為零金屬棒上電子受力為零,動能不變。因此拉力做功等於電子電位能改變。所以屬棒上電子受力為零,動能不變。因此拉力做功等於電子電位能改變。所以(17)式其實就是功能定理。請同學注意,拉力提供電子能量,磁力只是傳遞能量的媒介。
如果金屬棒在Δt時間內運動Δx距離,由(16)式可知電動勢大小為
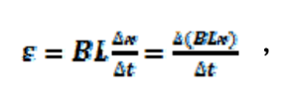 式(18)。
式(18)。其中Lx為金屬棒及金屬軌道所包圍的封閉矩形區域面積。我們定義BLx為通過封閉矩形區域的磁通量 ?。由(18)式可知電動勢大小等於磁通量對時間變化率。電動勢的方向由(1)式磁力方向決定。我們想用一個方程式決定電動勢的大小及方向。因此我們必須讓電動勢可為負數。我們用右手定則規定電動勢的正負號(圖五)。伸出右手,豎立大拇指,彎曲四指。大拇指沿磁場方向。如果電動勢產生的電流沿四指彎曲方向,則電動勢為正。反之則為負。在圖二中,磁場垂直軌道面向內,因此順時鐘方向的電動勢為正。金屬棒向右運動,磁通量對時間變化率Δ?/Δt為正,電動勢ε逆時鐘方向,因此為負。所以Δ?/Δt與ε異號。
我們得到動生電動勢的通量規則:
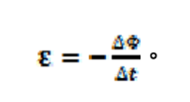 式(19)。
式(19)。若用微分學符號表示,則可寫為
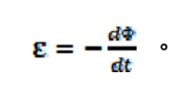 式(20)。
式(20)。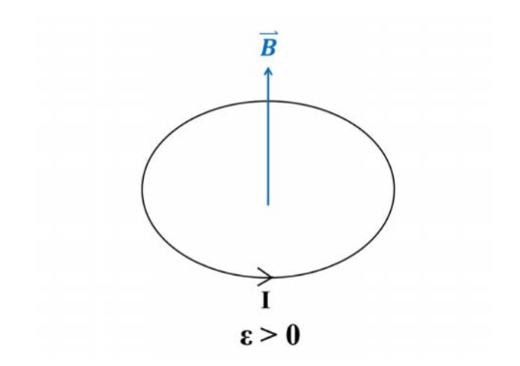 圖五。
圖五。同學如果想更進一步瞭解動生電動勢,請參考E. P. Mosca, Am. J. Phys. 42, 295 (1974).

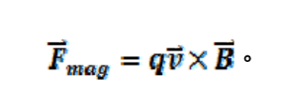 式(1)。
式(1)。
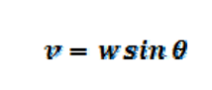
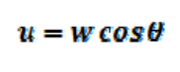
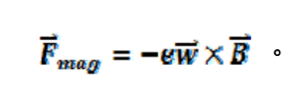
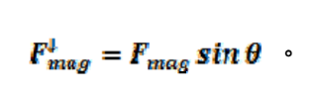
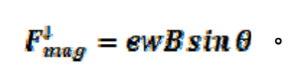 式(6)。
式(6)。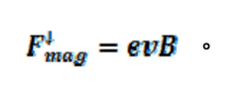 式(7)。
式(7)。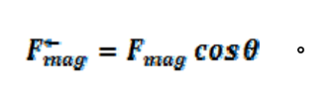
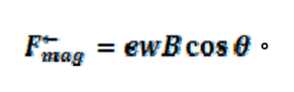
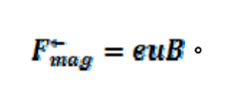 式(10)。
式(10)。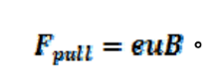
 圖三。
圖三。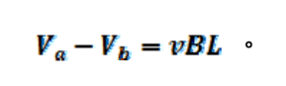
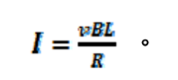 式(13)。
式(13)。
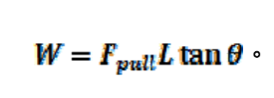
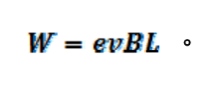
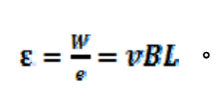
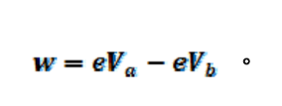
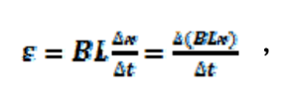 式(18)。
式(18)。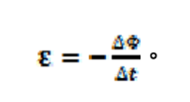 式(19)。
式(19)。