老師手中有一個玻璃瓶。將氣球放入瓶內,氣球吹氣口套在瓶口上。用打氣筒對氣球打氣使氣球膨脹。然後用橡皮塞塞住下面的瓶口。移開打氣筒,氣球的吹氣口雖然張開,氣球卻不會洩氣癟掉(圖一)。
 圖一。
圖一。以上演示與理想氣體狀態方程式有關。任何一個系統的狀態都可以用一些巨觀的狀態變數確定,例如溫度、質量、壓力、體積等。當所有狀態變數都不隨時間改變時,我們說此系統達到熱平衡。1662 年 Robert Boyle 發現當溫度固定時氣體的體積V與壓力P成反比:
PV = 常數 。 (固定溫度) (1)
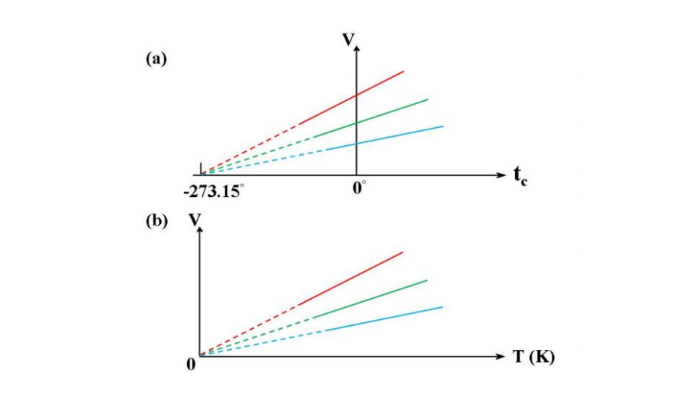
1800年左右 J. Charles與J. L. Gay-Lussac發現當壓力固定時氣體體積變化與溫度變化成正比。圖二(a)說明氣體體積與攝氏溫度ct的關係。不同顏色的直線代表不同氣體。圖二(a)有一個有趣的性質。不同顏色的直線做外插都會在-273.15°C 與溫度軸交會。這個性質似乎意謂如果氣體可被降溫至-273.15°C 則氣體體積為零。因此科學家認為-273.15°C 是最低溫度。我們將此溫度定義為絕對零度。以絕對零度為零點的溫標稱為絕對溫標或克氏溫標。克氏溫度T與攝氏溫度ct的關係為:
T = tc + 273.15 , (2)
其單位為 kelvins(K)。用克氏溫度表示,Charles 與 Gay-Lussac 定理可寫為:
V ? T 。 (固定壓力) (3)
圖二(b)說明氣體體積與克氏溫度的關係。直線通過原點。Gay-Lussac也發現當體積固定時氣體壓力改變與溫度改變成正比。用克氏溫度表示,
P ?T 。 (固定體積) (4)
方程式(1) (3) (4)可合併寫為:
PV T。 (5)
PV的數值與氣體分子數N有關。在固定溫度及壓力下,體積V與分子數N成正比。在固定體積及溫度下,壓力P與分子數N成正比。因此PV與N成正比。由此結果及(5)式我們得到理想氣體狀態方程式:
PV = NKT , (6)
其中K是波茲曼常數
K = 1.38 ×10-23? J/K
理想氣體狀態方程式也可以用氣體分子莫耳(mole 簡寫為 mol)數表示。一莫耳物質所含的原子數或分子數等於12 克碳-12 同位素所含的原子數。此數稱為亞佛加厥數:
NA = 6.02×1023mol-1
n莫耳氣體分子數為:
N = nNA??
因此理想氣體狀態方程式(6)可寫為:
PV = nRT, (7)
其中
R = KNA = 8.314 J/mol·K?
是通用氣體常數。
在本單元演示中,移開打氣筒前玻璃瓶內的氣體壓力為一大氣壓。移開打氣筒,氣球內的氣體壓力也為一大氣壓。氣球內外氣壓相同,氣球的彈力使氣球略為縮小,玻璃瓶內氣體體積略為增加。依據理想氣體狀態方程式,瓶內氣體體積增加,壓力減小。當瓶內氣體壓力加氣球彈力等於一大氣壓時,氣球不再縮小。所以雖然氣球吹氣口張開,氣球卻不會洩氣癟掉。
圖二。
