什麼是精準醫療?
你是否有過以下經驗?身體不舒服去給醫生看,描述自己這裡痛那裏怪的症狀給醫生聽,再追加抽血、驗尿或照超音波等常規檢查,接著醫生會依據這些線索和自身的經驗下診斷並給予處方,這是傳統醫學的流程。那什麼是所謂的「精準醫療」呢?其理念為在傳統的檢測之外再加上生物醫學檢測 (例如基因檢測、蛋白質檢測、代謝檢測等等),運用大數據的力量進行人體基因資料庫的比對分析,以利找到最適合的治療法,不僅減少醫療資源的浪費、將治療效果最大化,同時也減少不必要的副作用。為了達到精準醫療的目的,不再只是醫療界的醫護人員單打獨鬥,看似生冷的AI技術也能在此領域助上一臂之力,讓生命的發展有更多的可能性。
神奇的DNA序列
若是抽絲剝繭來看,人類的全身是由幾十兆的細胞所組成,細胞裡的細胞核內又包含著染色體,而染色體又是由像階梯的雙股螺旋所組成,這一階一階的就是所謂「鹼基對」。位於染色體上的DNA序列是由A、T、G、C這4種鹼基的線性排列組合,構成的生物遺傳訊息可以決定獨特的表現性狀。
為什麼每一個人都是獨一無二?
一般來說,在30億個鹼基對中,個人基因體與人類參考基因體約存在4~5百萬個變異 (variant),也就是說,兩個沒有親緣的個體之間約存在 0.1 % 的基因序列差異。在一個族群中,我們將超過 1% 以上人口擁有的變異稱之為單核苷酸多態性 (Single Nucleotide Polymorphism,SNP),依據美國國家生物技術資訊中心於2017年所釋出的SNP資料庫,人類共含有 113,862,023 個已驗證的 SNP。而正是這些變異造就你我在身高、髮色、血型甚至疾病等等的差異,我們將個人基因體上的變異資訊稱為基因型 (Genotype),表現於性狀上的差異稱之為表現型 (Phenotype),若能揭開基因型與表現型的關聯性,將有助於理解表現型的成因及機制,或可以將基因變異做為基因標記預測表現型。
全基因體關聯性分析GWAS
在過去的十多年,全基因體關聯性分析 (Genome-Wide Association Study,GWAS) 是探索每一個 SNP 與不同表現型 (疾病、癌症或藥物反應等等) 之間是否存有關聯性的一個簡單而有效的方法。GWAS是怎麼進行的呢?圖一是一個控制組 (Control) 與病例組 (Case) 各250人的GWAS資料集,GWAS首先對每一個SNP建立列聯表 (Contingency Table),如圖一左半,列聯表中大寫字母A與B分別表示SNP1與SNP2的主要基因型 (Major Allele),小寫字母a與b則分別為SNP1與SNP2的次要基因型 (Minor Allele),而列聯表中數字表示對應的人數 (因為人類有兩套染色體,同一個點位在兩個染色體上可能是不同基因型,在計算列聯表時其中一種做法是以基因型計次,所以列聯表加總會是人數的兩倍)。有了SNP 1與SNP 2的列聯表,就可以利用統計方法來檢測每一個SNP與疾病的關聯性,在這個極端的例子中,因為SNP 1的基因型在對照組與病例組間的數量沒有明顯的差異,SNP 1的基因型與疾病與否的關聯性不高,檢定會得到較大的P值 (P-Value)。相反地,在SNP 2中,所有帶有基因型B的人都為正常人,所有帶有基因型b的人都為病人,顯示SNP 2的基因型與疾病存有極大的關聯性,檢定會獲得極小的P值。GWAS 分析的最後一個步驟會將所有SNP的-Log10 (P-Value) 彙整在一起,並依照SNP於基因體上的相對位置繪製成曼哈頓圖 (Manhattan Plot),如圖一(c),曼哈頓圖的橫軸為人類 23 對染色體的座標,如此就能清楚地呈現與疾病有顯著關聯性的SNP之所在位置。通常GWAS會以-Log10 (P-Value)≧8為條件,來判斷SNP與疾病是否有顯著關聯性,如圖一(c) 中的第19號染色體有一個明顯的訊號。
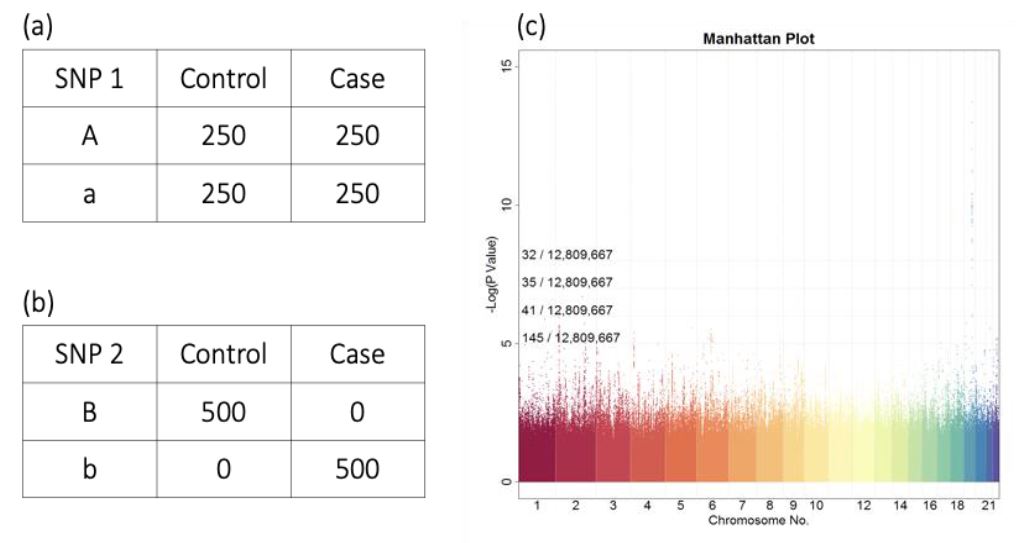
圖一、GWAS分析範例 。圖/臺灣大學陳倩瑜教授提供
美麗而浪漫的分析法存在著缺陷?何為上位作用?
據說,曼哈頓圖的命名由來是因為科學家看到GWAS -Log10 (P-Value) 的分佈像是曼哈頓的城市天際線,但在這個美麗而浪漫的分析方法背後其實存在不足,因為上述的GWAS採用單變量分析,也就是一次只考慮一個SNP與表現型之間的關聯性,這樣的分析忽略了基因變異之間的交互作用可能與表現型產生關聯,使得GWAS的成果局限於單基因 (Monogenic) 決定的表現型上。
我們稱上述影響表現型的基因交互作用為「上位作用」(Epistasis),上位作用普遍的存在於自然界之中。以圖二為例,拉布拉多犬有三種主要的毛色,黑色、棕色以及米色。這三種毛色被兩個色素基因點位所決定,分別是B (Brown) 和E (Extension色素分布),這兩個基因點位會直接影響色素表現進而產生不同毛色。從圖內可以看到這兩個基因點位的組合中,如果有任何一個顯性E,則毛色由B點位決定:如果有任一個顯性B,則毛色為黑色,若為兩個隱性b則為棕色;但若E點位為兩個隱性ee時,不論B點位的基因型為何都會是米色。E點位對於毛色的決定權凌駕於 B 點位之上,故稱為上位作用,而上述的 GWAS分析方法無法偵測這類交互作用的存在。
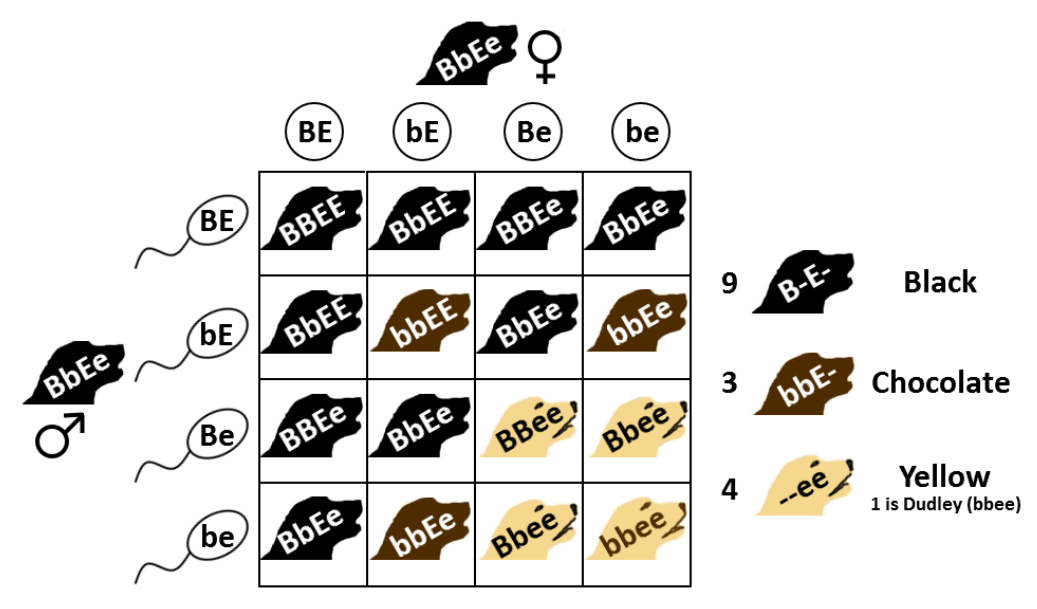
圖二、拉布拉多犬的毛色由兩的基因點位B (Brown) 和E (Extension) 的組合而決定,行列各自表示兩套染色體中的其中一套染色體上的基因型。圖/wikipedia
疾病之成因常是複雜的—由單基因疾病到複合疾病
一個基因變異就產生疾病,可稱為單基因疾病 (Monogenic Disease);若疾病由多個基因變異的交互作用所決定,則可稱為複合疾病 (Complex Disease),像是阿茲罕默症、第二型糖尿病,或是部分精神疾病等等。在數學上除了GWAS之外,我們可以用線性迴歸 (Linear Regression) 或羅吉斯回歸 (Logistic Regression) 來建立基因變異與疾病之間的關係。如圖三,我們可以想像喝到來自鉛管的水會導致疾病,SNP 變異與否表示鉛管上的開關是否開啟,權重α越大,可想像成鉛管越粗,亦即喝到污染的水越多,因此得到疾病的機率越高,反之亦然。因為單基因疾病只與一個基因變異有關,所以可以表示成y = αi × SNPi,其中i ∈ {1, 2, ..., SNP數}。
但是對於複合疾病,它像是多條不同粗細的鉛管有著各自獨立的開關,鉛管所有的水匯集成槽,罹病與否端看這個水槽的水位是否高過水閥。我們稱這樣的交互作用為累加式交互作用 (Additive Interaction),它很適合用圖中的羅吉斯回歸來表示之。但有時候基因變異間的交互作用並不是彼此獨立的關係,例如前述的上位作用則需要利用基因變異的相乘 αij × SNPi × SNPj 來建立模型,其中 i, j ∈ {1, 2, ..., SNP數} 且 i ≠ j 。在單變量分析時,兩個變異開關各自打開時流出的水量,可能少到會被GWAS所忽略,但如果兩個開關一起打開時便會一下子大幅增加罹病機率,這樣的交互作用稱為協同作用 (Synergistic Interaction),我們可以使用 Logit(Py) = α0 + αi×SNPi + αj×SNPj + αij×SNPi×SNPj 建立兩個基因點位完整的交互作用模型,其中Py為y的機率。但是若將這一個式子運用到全基因體的4~5百萬個點位,會面臨兩個很大的問題:計算複雜度以及統計檢定力。計算複雜度的問題在於必須展開基因變異的各種可能組合,導致維度的詛咒 (Curse of Dimensionality);另外一個挑戰是統計檢定力,因為計算這些數目龐大的統計檢定是根據高維度但是樣本數有限的資料,這些交互作用可能會跟表現型產生隨機的關聯性,因此會產生許多偽陽性 (False Positive) 的交互作用。
圖三、各種基因變異的交互作用及其與疾病之間的關聯。圖/臺灣大學陳倩瑜教授提供
以機器學習搭配基因資訊為基礎之上位作用偵測演算法—GenEpi
為了解決這些問題,由臺灣大學陳倩瑜教授帶領的機器學習與生物資訊研究團隊於2020年發表了一個以機器學習搭配基因資訊為基礎之上位作用偵測演算法— GenEpi,其核心概念是利用基因體上的功能片段來分割資料,進而降低資料維度。如圖四(b),基因變異資料依照基因被分割開來,接著基因上的基因變異的所有交互作用會被展開來如圖四(a),以兩個基因變異為例,總共會有3+3個累加式交互作用 (圖中紫色點),和9個協同作用 (圖中藍色點) 的變數被產生。各基因上的變數集會各自利用線性迴歸或羅吉斯回歸來建立模型,並引用穩定性選擇法 (Stability Selection),此法之概念是:在每一迴圈中針對樣本隨機取樣,每一次取樣會各自建立模型,一個變數必須於多數的模型都有夠大的權重才得以保留,如此便能降低偽陽性的發生。
圖四、論文“Genepi: Gene-Based Epistasis Discovery Using Machine Learning”所開發之GenEpi架構圖。圖/臺灣大學陳倩瑜教授提供
因此在階段一 (Stage 1) 的結尾可以看到,通過穩定性選擇法的變數才得以保留,另外有些基因沒有任何SNP變數通過篩選,該基因就不會進到下一個階段。在下一個階段 (Stage 2),GenEpi會利用通過篩選的 SNP 進一步產生跨基因的交互作用變數 (圖中綠色的點),沿用前一個階段的穩定性選擇法,所有與疾病關聯的基因變異交互作用可以被篩選完成。最後因為有些疾病與其他環境因子或是臨床變數有關,像是性別、年齡等,若資料集含有這些變數,GenEpi可以將之與篩選完的基因變數進行學習,產生最終模型。在模擬資料的結果中,GenEpi可以有效的偵測出模擬資料的協同作用,例如運用在阿茲罕默病人的資料上,GenEpi 可以偵測出已知的基因標記APOE上的SNP:rs429358,另外還偵測出多組顯著程度高 (P-Value < 10-6) 的基因變異交互作用,最終模型對於疾病與否的預測能力曲線下面積為0.85。這些結果佐證,透過機器學習的技術是可以幫助偵測疾病的致病基因變異。
GenEpi完美中的不完美
GenEpi仍然有其限制,譬如它只能偵測兩兩的交互作用,涵蓋三個以上基因變異的協同作用將無法被偵測;亦或是當資料集不足的時候,太寬鬆的篩選條件可能造成過度擬合(Overfitting),太嚴格的篩選條件則不會有任何的變數被留下。這些限制都還仰賴學者們持續改良進而突破限制,人工智慧和生技醫療擦出的火花,就等著你來創造。
本著作係採用 創用 CC 姓名標示─非商業性─禁止改作 3.0 台灣 授權條款 授權.
本授權條款允許使用者重製、散布、傳輸著作,但不得為商業目的之使用,亦不得修改該著作。 使用時必須按照著作人指定的方式表彰其姓名。
閱讀授權標章或
授權條款法律文字。